DFS vs BFS: Key Differences, Use Cases, and Examples
October 19, 2024
When working with graphs and trees, two fundamental algorithms comes to mind. Depth-First Search (DFS) and Breadth-First Search.
If you’ve ever wondered what the differences between DFS and BFS, you are in the right place. In this blog post I will try to breakdown DFS vs BFS, explain their key differences, use cases, and code samples in JavaScript.
What is Depth-First Search (DFS)?
DFS is one of the graphs traversal algorithms that explores as far as possible down one branch before backtracking. It’s like a person walking through a maze, who follows one path to the end before returning to explore other options.
Key Features of DFS:
- Traversal Type: Depth-First, explore one branch deeply before finding other options.
- Data Structure: Uses a stack (LIFO - Last In, First Out) to keep track of visited nodes.
- Use Cases: DFS is great for problems like solving maze, puzzles, or when we need to exhaustively explore all solutions before deciding.
What is Breadth-First Search (BFS)?
BFS is another fundamental graph traversal algorithm. Instead of going deep into one branch, it explores all possible neighbors at each level before moving deeper into the graph. Picture someone exploring a city by first visiting all streets directly connected to them before moving to the next level of streets.
Key Features of BFS:
- Traversal Type: Breadth-first (explores all neighbors at the same level first).
- Data Structure: Uses a queue (FIFO - First In, First Out) to maintain the order of nodes.
- Use Cases: BFS is ideal when you need to find the shortest path or finding the distance between nodes.
DFS vs BFS: Key Differences
| Features | DFS | BFS |
|---|---|---|
| Search Strategy | Goes deep into a branch before backtracking | Explores neighbors first, then their neighbors |
| Data Structure | Stack (LIFO) | Queue (FIFO) |
| Use Case | Good for deep recursive problems or exhaustive searches | Good for finding shortest paths and level-by-level exploration |
| Path Finding | May not find the shortest path | Guarantees shortest path |
| Memory Usage | Can use less memory in some cases | May require more memory as it holds all nodes at the current level |
| Performance | Depends on graph structure O(n+m) | Similar complexity O(n+m) |
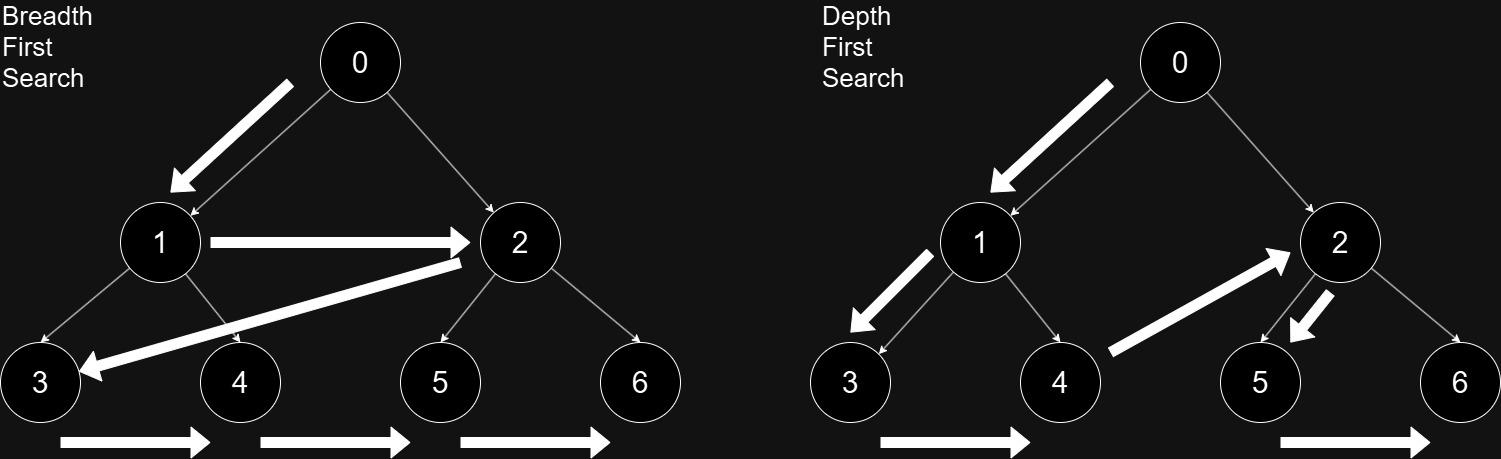
Visualizing DFS and BFS
Below is a simple illustration of DFS and BFS in graph traversal:
DFS Example:
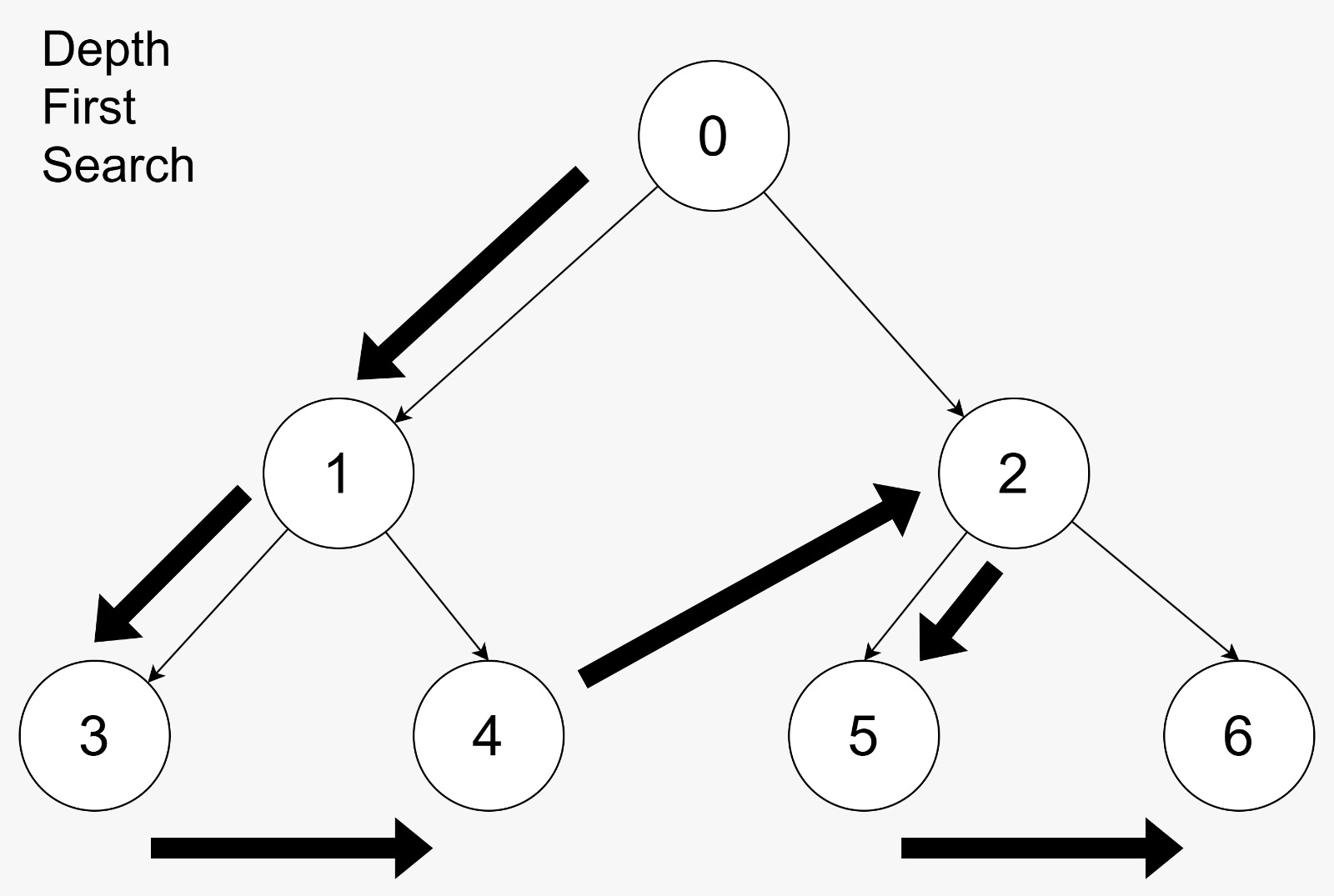
- Start at node
0 - Visit node
1, then deep to node3and next node4 - Once we hit the leaf (end) node, backtrack and visit node
2, then visit node5, and then node6
BFS Example:
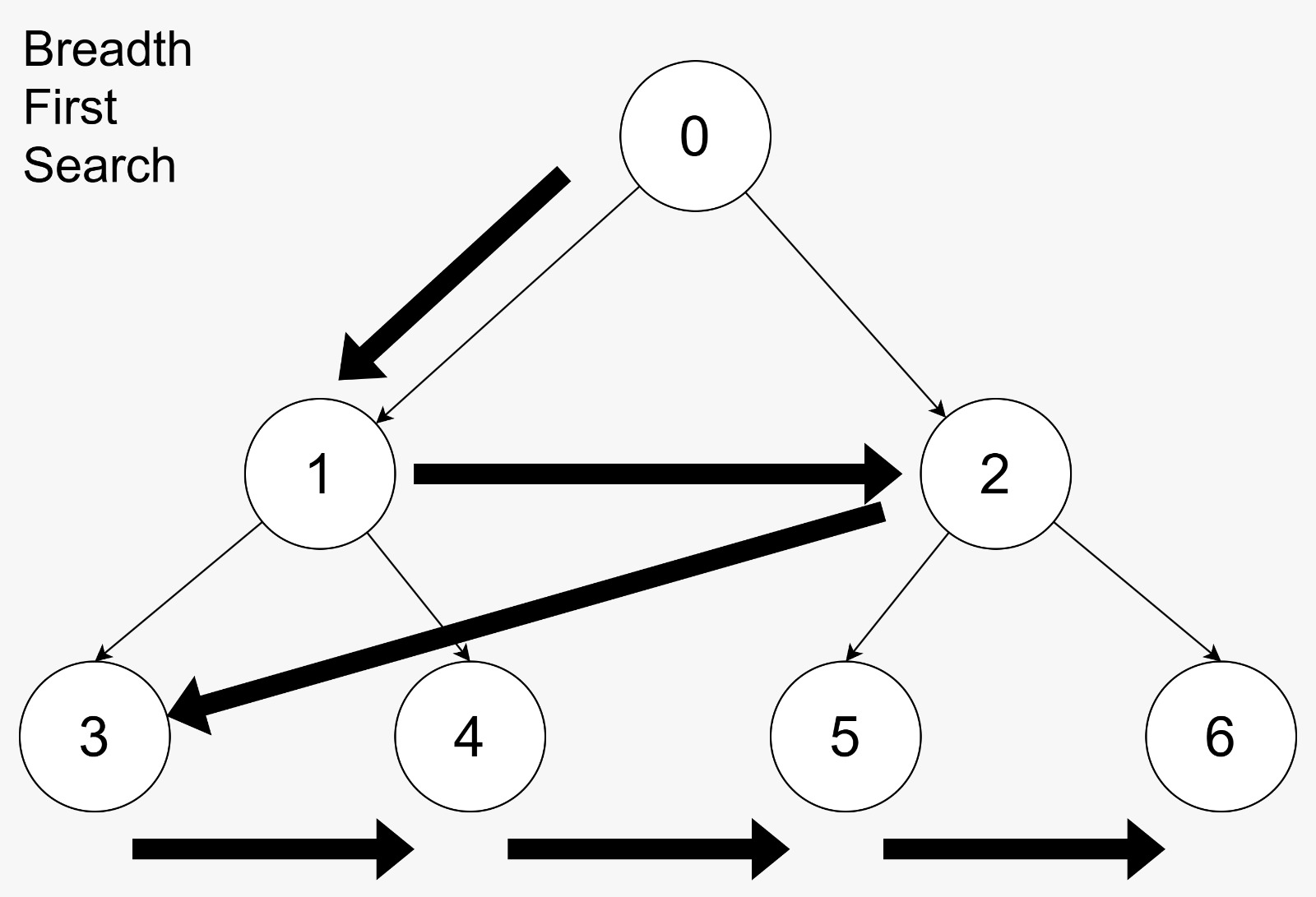
- Start at node
0 - Visit node
1, then to node2 - Visit next level node
3, then node4, then node5, and finally node6
DFS and BFS Code Examples in JavaScript
Let’s implement DFS and BFS using JavaScript
DFS Implementation in JavasScript
const graph = {
A: ['B', 'E'],
B: ['A', 'C'],
C: ['B', 'D', 'F'],
D: ['C'],
E: ['A'],
F: ['C']
};
function dfs(graph, node, visited = new Set()) {
visited.add(node);
console.log(node);
for (let neighbor of graph[node]) {
if (!visited.has(neighbor)) {
dfs(graph, neighbor, visited);
}
}
}
// Run DFS starting at node 'A'
dfs(graph, 'A');
// result A -> B -> C -> D -> F -> EBFS Implementation in JavaScript
const graph = {
A: ['B', 'E'],
B: ['A', 'C'],
C: ['B', 'D', 'F'],
D: ['C'],
E: ['A'],
F: ['C']
};
function bfs(graph, start) {
const queue = [start];
const visited = new Set();
visited.add(start);
while (queue.length > 0) {
const node = queue.shift();
console.log(node);
for (let neighbor of graph[node]) {
if (!visited.has(neighbor)) {
visited.add(neighbor);
queue.push(neighbor);
}
}
}
}
// Run BFS starting at node 'A'
bfs(graph, 'A');
// result A -> B -> E -> C -> D -> FWhen to use these algorithm?
When to Use DFS:
- You need to explore all possible paths (e.g., in puzzle-solving).
- When you’re dealing with deep graphs where exploring down a path is beneficial.
When to Use BFS:
- You want to find the shortest path in an unweighted graph (e.g., in routing problems).
- You need to explore nodes level by level, like in social networks or when computing the shortest distance between two nodes.
Conclusion
Both DFS and BFS are indispensable tools for graph traversal. Knowing the difference between DFS and BFS helps you choose the right tool for the task at hand. Whether you’re navigating a complex maze (DFS) or searching for the shortest route (BFS), these algorithms provide efficient ways to explore the nodes and edges of any graph.
FAQ
1. Which is faster, DFS or BFS?
Both algorithms have the same time complexity of O(N+M) in general, where N is the number of vertices and M is the number of edges. However, BFS is typically better suited for finding the shortest path in unweighted graphs.
2. Does DFS guarantee the shortest path?
No, DFS doesn’t guarantee finding the shortest path. It’s focused on exploring as far as possible down one branch before backtrack.